ボリンジャーバンドは標準偏差というテクニカル分析にはあまり聞き慣れない計算式を用いて相場を視覚的に判断するインジケーターとして非常に人気のあるもので、計算式から本質的なボリンジャーバンドの性質を見て、トレード判断に生かしていく事が大切になってくる。
ボリンジャーバンドは1本の移動平均線と数本のバンドで構成されていて、全て表示させると下のような表示になるが、基本的には2σというバンドを使用する。下チャートがボリンジャーバンドの基本的なラインの読み方になるので覚えておいて欲しい。
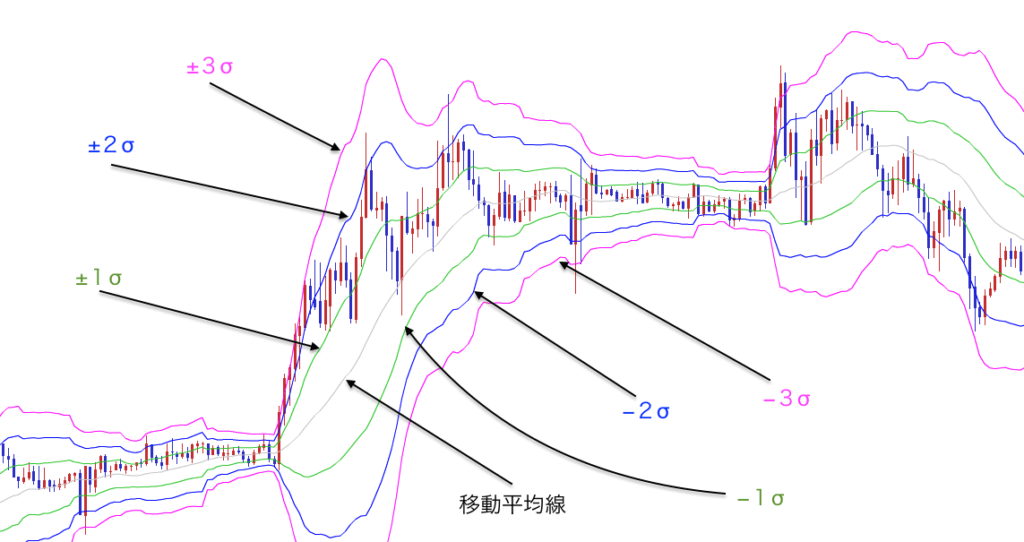
移動平均線を中心にして外側に向かって数本のライン(波動)が表示されているが、これは標準偏差をもとに計算されたもので、±1σ 2σ 3σ(シグマ)と読む。基本的にこのライン構成でボリンジャーバンドは成り立っているが、ボリンジャーバンドを知る為には、その基本的な計算式となる「標準偏差」について知る必要があるので、これから説明していきたいと思う。
ボリンジャーバンド計算式と値動きの確率
ではボリンジャーバンドの基本となる標準偏差と、その標準偏差から見る値動きの確率について説明していこう。
標準偏差
標準偏差が使われている身近なものとしては、中学高校などの試験の成績の値をわかりやすく示す指標として「偏差値」というものがある。
偏差値は50を平均値としてどのくらい自分の成績が平均からどのくらい乖離した場所に位置しているのかを見るものだ。
偏差値は次のような計算式で算出されている。
偏差値=(自分の点数−平均点)÷標準偏差×10+50
標準偏差とは、自分の点数から平均点を引いた数字を標準偏差で割るというもので、とあるデータの中でばらついている数値(分散)の度合いだ。数値が散らばっていればいるほどその範囲は大きくなり、散らばっている数値が低くまとまりがあるほどその範囲は小さくなる。
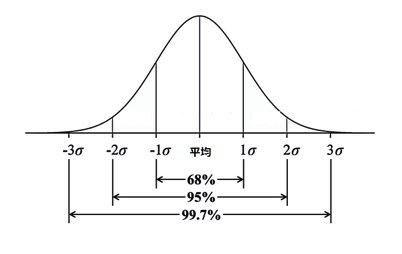
つまり分散の度合いが低いと上記の図の山が低くなり、分散の度合いが大きいと山が高くなる。そして標準偏差で割った数字を10倍する。
これは算出されて出てきた数値が小さいので、単純に考えやすくするために10倍にしているが、最後に標準である基準数字50をかけると偏差値が算出される。
この偏差値の計算式から見た場合に考える事は、みんなの点数があまり変わらない水準にある時は標準偏差の点数の範囲もグッと縮小するという事になる。この計算式がもたらす性質とは次の理論値になる。
| 偏差値の範囲 | 全体の割合 |
|---|---|
| 45〜55の範囲内 | 全体の約38.3% |
| 40〜60の範囲内 | 全体の約68.3% |
| 35〜65の範囲内 | 全体の約86.6% |
| 30〜70の範囲内 | 全体の約95.5% |
標準偏差から見る値動きの確率
この偏差値をボリンジャーバンドに当てはめて考えていこう。ボリンジャーバンドではこの偏差値50を真ん中のラインである「移動平均線の位置」で表し、値動きの確率を見ていくものになる。
バンドの範囲内に値動きが収まる可能性を%化して、理論値をボリンジャーバンドに当てはめると次のようになる。
- ±1σの範囲の中に値動きが収まる確率が68.3%
- ±2σの範囲の中に値動きが収まる確率が95.5%
- ±3σの範囲の中に値動きが収まる確率は99.7%
σ(シグマ)というのが標準偏差を表している記号だ。
しかしこの標準偏差だが、対象の数が増えると世の中の正規分布に従う確率が上がるという性質を利用しているので、参加数が少ない株式市場の新興市場銘柄など、参加者が少なくなるほど参考になりにくいという特徴があるので覚えておこう。
逆に為替市場や東証一部銘柄など市場参加者が多くなればなるほど参考価値の高いものになっていく。
ボリンジャーバンドの期間設定
基本的にボリンジャーバンドの期間設定は基準となる中心の移動平均線と標準偏差の値の2つだ。
移動平均線の期間設定
移動平均線の設定に関しては基本的に20日、21日を使用している人がほとんどだ。
分析ツールのデフォルトでも20日設定になっているものがほとんどで、20日と21日どちらが良いのかと言えば、20日で良い。21日の定義というのは1ヶ月で平均すると21日くらいの平均で市場が開いているので、過去1ヶ月間の値動きということで、21日と言っているだけだ。
ボリンジャーバンドは標準偏差を使って価格の偏差値を見る事にあるので、この1日のズレはまず支障はなく、こだわる必要性は全くない。
標準偏差の設定
移動平均線の他に標準偏差や偏差という設定項目があるが、これは基準となる移動平均線が20日設定なら2σ1本で大丈夫だ。その基準が1番ボリンジャーバンドの有効性が発揮できる基本となる。
なぜ1σを表示させないのか?というのは、先ほどの標準偏差の理論値では1σまでの値動きの確率は68.3%。もちろんトレードスタイルにもよるが、68.3%の中で何を見ていくのかという事になると、値動きを判断するにはアバウトすぎる確率だし、そもそもインジケーターは必要最小限のものだけを表示させていたほうが分析する際にも優位性がある。
インジケーターはなんでもかんでも表示させていれば良いというものではない。
そして2σが95.5%で3σが99.7%の中に価格が収まる可能性だが非常に確率が近い。では3σを表示させる必要性はあるのだろうか?という事にもなる。
もちろん表示させたほうが自分にとっては良いと思うならそれもいいだろう。何を表示させて何をどう使うかはもちろんトレーダー次第だからだ。あくまでも参考程度のアドバイスとして考えてもらえたらいいだろう。
標準偏差というのはあくまで正規分布の範囲内で収まる可能性であって必ず99.7%の中で収まるものではないし、相場の中でこの値を抜けていく事も普通にある。
2σは外せないものだが、他の1σと3σに関してはお好みで、どうしても3本の標準偏差が表示させたいという方は、ボリンジャーバンドを3つ表示という事になる。
まとめ
今回はボリンジャーバンドの計算式から見た基本知識を中心にお話ししたが、ボリンジャーバンドのチャート分析に関してはボリンジャーバンドの基本的なチャート分析の特徴とはの記事で紹介しているのでチェックしてみてほしい。
ボリンジャーバンドは標準偏差を用いた非常に優秀なテクニカル分析手法だ。しかし、注意しないといけない思い込みは、標準偏差の%の数字の中に価格が確実に収まるという事を前提に考える事だ。
テクニカル分析でありがちな、ここのラインまできたら買いサインだから買おうとか、ここのラインにぶつかったら逆張りサインでエントリーだとか、そういう小手先のエントリーだけでは継続して勝つのはやはり難しい。
もちろん値動きを分かった上でなら話は別だ。
あくまでも過去20日の限定された過去から算出された標準偏差の値から、確実に3σ以内に収まるという保証はどこにもない。
テストの点数であれば上限が100点と決まっているかもしれないが、相場の値動きはそういう確定した理屈はなく、100%が基本的に上限だったとしても、120%にもなる事があるのが相場だ。